In the case of boilers, the desired output is heat, and the necessary input is fuel. The thermal efficiency of a boiler can be expressed as the instantaneous rate of heat output divided by the instantaneous rate of fuel consumption, where both quantities are expressed in the same units — usually Btu/hr.
Similar definitions of thermal efficiency can be developed for other heat sources, such as heat pumps or solar thermal collectors.
While the thermal efficiency of heat sources is important in achieving low operating cost and conserving fuel, it is not the only efficiency that should be considered by heating system designers.
The energy required to distribute the heat produced by any heat source, or the cooling effect generated by any cooling source, should also be considered. Systems that use a significant amount of electrical energy to move heat from where it is produced to where it is needed in the building, even when that heat is produced at high thermal efficiency, are undesirable. This also holds true for any kind of cooling system.
One way to assess and compare this aspect of system design is to define “distribution efficiency” as follows:
Formula 6-1:
$$n_d={Q_{delivered}\over W_e}$$
Where:
$n_d$ = distribution efficency (Btu/hr/watt)
$Q_{delivered}$ = rate of heat delivery (Btu/hr)
${W_e}$ = electrical power required by the distribution system (watts)
The higher the distribution efficiency, the lower the operating cost of the distribution system.
For example: Consider a zoned hydronic system with four circulators. Each circulator requires 75-watt power input when operating. At design load, with all four circulators operating, the system delivers 100,000 Btu/hr to the building.
The distribution efficiency of this system at design load conditions would be:
$$n_d={Q_{delivered}\over W_e}={100,000{Btu\over hr}\over 4 \ times 75watt}=333.3{Btu/hr\over watt}$$
The number 333.3 Btu/hr/watt can be interpreted as follows: For each watt of electrical power supplied to the distribution system, that system delivers 333.3 Btu/hr to the building.
However, this number means little without something to compare it to. To provide a comparison, consider a forced-air furnace with a blower that requires 550 watts while delivering 80,000 Btu/hr to the building. The distribution efficiency of that system is:
$$n_d={Q_{delivered}\over W_e}={80,000{Btu\over hr}\over 550watt}=145.5{Btu/hr\over watt}$$
In this comparison, the forced-air system has less than half the distribution efficiency of the hydronic system. This implies that the forced-air system will require over twice the electrical energy as the hydronic system to deliver the same amount of heat to the load.
The concept of distribution efficiency can be used to compare competing hydronic system designs.
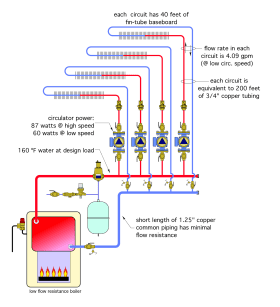
Imagine that the four-zone system cited in the previous example is configured as shown in Figure 6-1.
Each zone is assumed to have an equivalent length of 200 feet of 3/4” copper tubing. Each zone circuit contains 40 feet of fin-tube baseboard and is equipped with a 3-speed circulator operating on high speed with an electrical power input of 87 watts. The supply water temperature to all zone circuits is 160ºF. Assume the system’s heat source and headers have very low head loss, and thus provide good hydraulic separation between the zone circulators.
This system can be simulated to find its thermal and hydraulic equilibrium operating conditions. The results of this simulation indicate the flow rate in each zone will be about 6 gpm, and total heat output of the baseboard in each zone is 12,675 Btu/hr.
The distribution efficiency of this system with all four zones operating is:
$$n_d={Q_{delivered}\over W_e}={(4 \times 12,675){Btu\over hr}\over (4 \times 87)watt}=146{Btu/hr\over watt}$$
If the circulator is changed from its high-speed to lowspeed setting, the input power drops to 60 watts, and the zone flow rates drop to about 4 gpm each. The heat output of each zone also drops to 12,310 Btu/hr. The distribution efficiency is now:
$$n_d={Q_{delivered}\over W_e}={(4 \times 12,310){Btu\over hr}\over (4 \times 60)watt}=205{Btu/hr\over watt}$$
In this case, reducing the zone circulator speed from high to low reduced the electrical power required by 31% and heat output by only 2.9%. Thus, the higher flow rate produced a very small gain in heat output. In this example, operating the circulators on their low-speed setting increased distribution efficiency by 40%.
If each zone circulator was set to low speed and operated for 3,000 hours per year, the total electrical energy used by the distribution system would be:
$$4(60 watt)({3000hr\over yr})({1kwhr\over 1000watt \times hr})= 720kwhr/yr$$
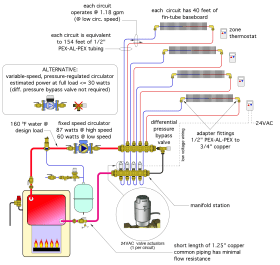
This system can also be compared to a system using a single fixed-speed circulator to supply four zones, each regulated by a manifold valve actuator. A schematic for this system is shown in Figure 6-2.
Each zone circuit contains the same 40 feet of 3/4” fin-tube baseboard, as well as 150 feet of 1/2” PEX-ALPEX tubing. With the single circulator on high speed (87 watts), the heat output of each zone circuit is simulated to be 11,221 Btu/hr and the flow rate through each zone is 1.76 gpm. The distribution efficiency of the system with all four zones operating is:
$$n_d={Q_{delivered}\over W_e}={(4*11,221){Btu\over hr}\over (87)watt}=516{Btu/hr\over watt}$$
If the circulator is switched to low speed (60 watts), each zone delivers 10,521 Btu/hr, on a flow of 1.18 gpm. The distribution efficiency now becomes:
$$n_d={Q_{delivered}\over W_e}={(4*10,521){Btu\over hr}\over (60)watt}=701{Btu/hr\over watt}$$
To make the comparison fair, the operating hours of the zone valve-based system must be increased so that it delivers the same total seasonal heat output as the system using zone circulators. This is done by multiplying the operating hours of the zone circulator system by the ratio of the design output of a zone circuit in the system using zone circulators, to that of a zone circuit in the system using zone valves. The total electrical energy use of the 60-watt circulator in the system using zone valves is now determined:
$$1(60 watt)({3000hr\over yr})({1kwhr\over 1000watt*hr})({12,310 Btu/hr\over 10,521 Btu/hr})= 211kwhr/yr$$
In this comparison, the system using zone valves delivers the same total heat using only 29% of the electrical energy required by the system using zone circulators. This demonstrates a distinct advantage of valve-based zoning from the standpoint of distribution efficiency and electrical energy consumption.
If a pressure-regulated circulator with ECM motor was used in combination with the valve-based zoning, and that circulator was operated in a constant differential pressure mode, the estimated electrical energy use would drop by at least 60%. This would put the estimated seasonal electrical energy use of the zone valve system at about 85 kwhr/yr.
At full speed, the power input to an ECM-circulator with the same head/flow characteristics as the previously described 60-watt circulator with PSC motor would be about 50% lower (e.g., about 30 watts). The estimated distribution efficiency of this system under design load conditions would therefore be:
$$n_d={(4*10,521){Btu\over hr}\over (30)watt}=1402{Btu/hr\over watt}$$
By using state-of-the-art products and careful design, it is possible to create hydronic distribution systems that have distribution efficiencies of at least 3,000 Btu/hr/watt.
Superior distribution efficiency is often the “untold story” regarding use of hydronic heating or cooling. Too often, a comparison of hydronic heating or cooling emphasizes the thermal efficiency of the heating or cooling source in comparison to that of a competing system, such as a forced-air furnace or air-to-air heat pump. Currently available condensing-capable forced-air furnaces will usually have thermal efficiencies that are equal to or slightly higher than that of mod/con boilers. This is largely due to lower return air temperatures to the furnaces compared to the lowest practical return water temperatures to mod/ con boilers or hydronic heat pumps.
Deciding to use a system that includes a heat source with incrementally higher thermal efficiency, at the expense of much lower distribution efficiency, can cause the total operating cost to be higher. Hydronic heating professionals should emphasize the energy savings associated with the low distribution energy requirements of well-designed hydronic systems.